Logarithmically convex function

In mathematics, a function f defined on a convex subset of a real vector space and taking positive values is said to be logarithmically convex or superconvex^[1] if 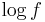$\log f$ is a convex function.

A logarithmically convex function f is a convex function since it is the composition of the increasing convex function 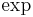$\exp$ and the convex function 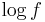$\log f$ , but the converse is not always true. For example 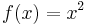$f(x) = x^2$ is a convex function, but 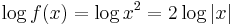$\log f(x) = \log x^2 = 2 \log |x|$ is not a convex function and thus 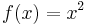$f(x) = x^2$ is not logarithmically convex. On the other hand, 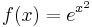$f(x)=e^{x^2}$ is logarithmically convex since 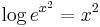$\log e^{x^2} = x^2$ is convex. An important example of a logarithmically convex function is the gamma function on the positive reals (see also the Bohr–Mollerup theorem).

References

^ Kingman, J.F.C. 1961. A convexity property of positive matrices. Quart. J. Math. Oxford (2) 12,283-284.

John B. Conway. Functions of One Complex Variable I, second edition. Springer-Verlag, 1995. ISBN 0-387-90328-3.

This article incorporates material from logarithmically convex function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.